Introduction
Here we will see example on binary tree using pointer in C programming language. The same concept can be used in other language to write program for binary tree.
What is Binary Tree?
Binary tree is an important class of tree in data structure. A node in binary tree can have at most two children, which are called sub-trees. Children of a node in binary tree are ordered. One child is called left child and another child is called right child.
A binary tree can be defined as
- an empty tree is a binary tree
- a binary tree consists of a node is called root, a left and right sub-tree both of which are binary trees once again.
Height of the Binary Tree
The height of a binary tree is “the maximum level of any node of a binary tree”.
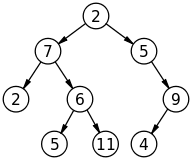
For example, in the above image the height of the binary tree is 4.
Binary Tree Traversal
Traversing is a process of visiting every node in the tree exactly once. Therefore, a complete traversal of a binary tree implies visiting the nodes of a tree in some linear sequence. These traversals are known as Inorder, Preorder and Postorder tree traversal.
If a tree T is traversed in Inorder fashion then left sub-tree of T is traversed first, then the root node of T is visited and then finally right sub-tree of T is traversed.
If a tree T is traversed in Preorder fashion then the root node of T is visited first, then the left sub-tree of T is traversed and finally right sub-tree of T is traversed.
If a tree T is traversed in Postorder fashion then the left sub-tree of T is traversed, then right sub-tree of T is traversed and finally the root node of T is visited.
Example with Source Code
The complete source code is given below:
/*
* File: BTree.c
* Author: https://roytuts.com
*/
#include <stdio.h>
#include <stdlib.h>
typedef struct bNode {
int data;
struct bNode *left;
struct bNode *right;
} bNode;
void insert(bNode **tree, int data) {
bNode *temp, *previous, *current;
if (*tree == NULL) {
temp = (bNode *) malloc(sizeof (bNode));
temp->data = data;
temp->left = temp->right = NULL;
*tree = temp;
return;
}
if (data < (*tree)->data) {
insert(&(*tree)->left, data);
} else if (data > (*tree)->data) {
insert(&(*tree)->right, data);
}
}
void delete(bNode *root) {
if (root != NULL) {
delete(root->left);
delete(root->right);
free(root);
}
}
bNode* search(bNode **tree, int data) {
if (*tree == NULL) {
return NULL;
}
if (data < (*tree)->data) {
search(&((*tree)->left), data);
} else if (data > (*tree)->data) {
search(&((*tree)->right), data);
} else if (data == (*tree)->data) {
return *tree;
}
}
void preorder(bNode *root) {
if (root != NULL) {
printf("%d\n", root->data);
preorder(root->left);
preorder(root->right);
}
}
void inorder(bNode *root) {
if (root != NULL) {
inorder(root->left);
printf("%d\n", root->data);
inorder(root->right);
}
}
void postorder(bNode *root) {
if (root != NULL) {
postorder(root->left);
postorder(root->right);
printf("%d\n", root->data);
}
}
int main() {
int choice, value;
bNode *root = NULL;
printf("\n:: Binary Tree using Linked List ::\n");
while (1) {
printf("\nChoose from below Menu\n");
printf("1. Insert\n2. Delete Tree\n3. Search in Tree\n4. Display preorder\n5. Display inorder\n6. Display postorder\n7. Exit\n");
printf("\nEnter your choice: ");
scanf("%d", &choice);
switch (choice) {
case 1: printf("Enter the value to be inserted: ");
scanf("%d", &value);
insert(&root, value);
break;
case 2: delete(root);
break;
case 3: printf("Enter the value to be searched in the tree: ");
scanf("%d", &value);
bNode *node = search(&root, value);
if (node != NULL) {
printf("\nSearched node found => %d\n", node->data);
} else {
printf("\nData Not found in tree.\n");
}
break;
case 4: preorder(root);
break;
case 5: inorder(root);
break;
case 6: postorder(root);
break;
case 7: exit(0);
default: printf("\nWrong selection!!! Please try again!!!\n");
}
}
}Testing
Executing the above C file will display the following output:
:: Binary Tree using Linked List ::
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 1
Enter the value to be inserted: 9
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 1
Enter the value to be inserted: 4
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 1
Enter the value to be inserted: 15
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 1
Enter the value to be inserted: 6
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 1
Enter the value to be inserted: 12
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 1
Enter the value to be inserted: 17
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 1
Enter the value to be inserted: 2
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 4
9
4
2
6
15
12
17
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 5
2
4
6
9
12
15
17
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 6
2
6
4
12
17
15
9
Choose from below Menu
1. Insert
2. Delete Tree
3. Search in Tree
4. Display preorder
5. Display inorder
6. Display postorder
7. Exit
Enter your choice: 7From the above output it is obvious that you can choose any option to proceed for binary tree operation. When you do not want to perform any operation on binary tree then you can choose option 7 to exit.
Source Code
Thanks for reading.